The model is based on the approach of Monteith[ 1972, 1977] and Kumar and Monteith [ 1981].It considers in stantaneous NPP (called P in the formulae) as a fraction of the incoming solar energy stored in to organic dry matter.
In brief,the model calculates a pure seasonal cycle of net biosphere–atmosphere fluxes as the difference of two fluxes inany month at each 
land grid cell,
F = H - NPP
where F is the net flux to the atmosphere, H is the heterotrophic respiration, and NPP is the net primary productivity.
The calculation is performed on the basis of measured Normalized Differential Vegetation Index (NDVI), incoming solar radiation, and surface temperature. There is an additional time-dependent water-stress term a, which may limit the efficiency either of NPP, or heterotrophic respiration, or both. This factor will be included in various of the calculations in this work in either of the two fluxes H and NPP; in the case described below, it is included in both.
NPP is calculated for each month as
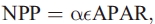
where APAR is absorbed photosynthetically active radiation and 
is a light-use efficiency parameter. APAR is computed from NDVI data by Gallow [1992] and incoming solar radiation inferred from cloudiness data by Leemans and Cramer [1991] using the method of Linacre [1968].
Heterotrophic respiration H is calculated as an exponential function of temperature as
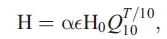
where 
is the heterotrophic respiration rate at T = 0 and 
(i.e., no water stress) and Q10 is the ratio of respiration at T + 10 to that at T; T is given in °C. We have absorbed 
into the formulation of H for later convenience.
In order to ensure a balanced biosphere (no net annual flux), we rescale H0 at each grid cell so that integrated NPP and H are equal over a year. Thus H0 is not a free parameter.
The water-stress factor, a = AET/PET (actual divided by potential evapotranspiration), is computed with the model of Prentice et al. [1993]. PET is assumed equal to equilibrium evapotranspiration, and AET is the minimum of PET and a supply rate assumed proportional to soil moisture. The model neglects the effect of soil freezing and snow accumulation, so that at low ambient temperatures where PET is mostly small, a tends toward 1. Freezing-induced drought effects are therefore not considered in SDBM; low temperatures rather affect H through its temperature dependence given by the value of Q10.
We can now write the total flux as
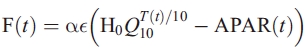Subject to the constraint that
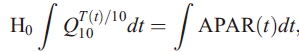
where integrals are taken over the annual cycle. Integrals are calculated as sums of monthly values weighted by the length of the month.
{{htmlJSON.LinkResourceFromRepositoryOrCreate}}{{htmlJSON.create}}.
{{htmlJSON.authorshipSubmitted}}
| Title | Author | Date | Journal | Volume(Issue) | Pages | Links | Doi | Operation |
|---|
Authors: {{articleUploading.authors[0]}}, {{articleUploading.authors[1]}}, {{articleUploading.authors[2]}}, et al.
Journal: {{articleUploading.journal}}
Date: {{articleUploading.date}}
Page range: {{articleUploading.pageRange}}
Link: {{articleUploading.link}}
DOI: {{articleUploading.doi}}
The article {{articleUploading.title}} has been uploaded yet.
| Title | Author | Date | Journal | Volume(Issue) | Pages | Links | Doi | Operation |
|---|
Authors: {{articleUploading.authors[0]}}, {{articleUploading.authors[1]}}, {{articleUploading.authors[2]}}, et al.
Journal: {{articleUploading.journal}}
Date: {{articleUploading.date}}
Page range: {{articleUploading.pageRange}}
Link: {{articleUploading.link}}
DOI: {{articleUploading.doi}}
The article {{articleUploading.title}} has been uploaded yet.
{{item.name}}
.
{{item.suffix}}
.{{item.suffix}}
{{htmlJson.LinkRelatedFromRepositoryOrCreate}}. {{htmlJson.CreateNew}}>
