Tensor Decomposition Model on Sharing Bicycles

A tensor is a multidimensional array that can be seen as an extension of a matrix in high dimensions (Kolda et al. 2009). In this research, the Tucker decomposition model under nonnegative constraints is used to process the third-order origin and destination tensors of shared bicycles.

Sharing BicyclesTensor DecompositionTraffic

true

Contributor(s)
Initial contribute: 2019-10-14

Authorship

  • 曹敏
    • :  
    南京师范大学地理科学学院
    :  
    caomin@njnu.edu.cn
    Is authorship not correct? Feed back

    Classification(s)

    ● Application-focused categoriesHuman-perspectiveSocial activities

    Detailed Description

    English {{currentDetailLanguage}} English
    The public bike-sharing (PBS) system has received increasing attention as a potential way to improve the first and last mile connections to other modes of transit and lessen the environmental impact of transportation activities (DeMaio, 2009; Ruch et al., 2014). Recently, an increasing number of cities have deployed bicycle-sharing systems to solve the first/last mile connection problem, generating a large quantity of data. Additionally, commuting regularities are usually linked to the spatial distribution or the transfer routing of bikes. In this theme, we come up with two models based on mathematical theory aiming to recognize the patterns in sharing bicycle data.
    • Tensor Decomposition
    A tensor is a multidimensional array that can be seen as an extension of a matrix in high dimensions (Kolda et al. 2009). In this research, the Tucker decomposition model under nonnegative constraints is used to process the third-order origin and destination tensors of shared bicycles.
    The purpose of the Tucker decomposition model is to decompose n-dimensional tensorM∈RI1xI2x...xIninto a n-dimensional core tensorG∈RJ1xJ2x...xJn. Factor matrices can be thought of as the principal components in each dimension of the tensor, and core tensor shows the level of interaction between the different components (Khoromskij et al. 2007). Taking a three-dimensional tensor as an example, the schematic diagram of Tucker decomposition model is shown in Figure 1. The three-dimensional tensorM∈RI1xI2xI3is decomposed into a core tensorG∈RJ1xJ2xJ3and three factor matricesA(1)∈RI1xJ1,A(2)∈RI2xJ2,A(3)∈RI3xJ3. The formula of Tucker decomposition is shown in equation (1).

    Figure 1. Illustration of the Tucker decomposition model (Cichocki et al. 2015)

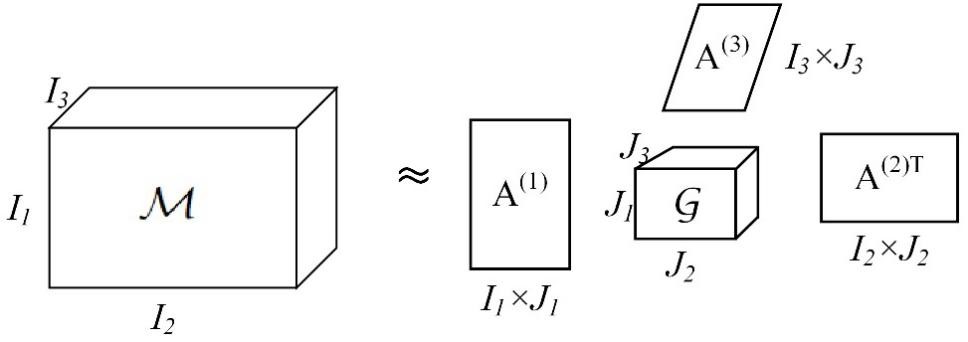
    Figure 1. Illustration of the Tucker decomposition model (Cichocki et al. 2015)

    M≅G x 1A(1) x 2A(2) x 3A(3)················(1)
    Where is a three-dimensional tensor; is a three-dimensional core tensor;A(1),A(2) andA(3)are three factor matrices.

     

    Each dimension represents a sort of pattern, three patterns can be found after tensor decomposition. The following figure (Figure 2) is the flow chart of Tensor Decomposition.

    Figure 2. Flow chart of Tensor Decomposition

    Figure 2. Flow chart of Tensor Decomposition

    Reference:

    DeMaio, P. (2009). Bike-sharing: History, impacts, models of provision, and future. Journal of public transportation, 12(4), 3.

    Banerjee, S., & Roy, A. (2014). Linear algebra and matrix analysis for statistics. New York: Chapman and Hall/CRC.

    Kolda, T. G., and Bader, B. W. 2009. Tensor decompositions and applications. SIAM review, 51(3), 455-500. 

    Khoromskij, B., and Khoromskaia, V. 2007. Low rank Tucker-type tensor approximation to classical potentials. Open Mathematics, 5(3), 523-550.

    View Full Text

    模型元数据

    {{htmlJSON.HowtoCite}}

    曹敏 (2019). Tensor Decomposition Model on Sharing Bicycles, Model Item, OpenGMS, https://geomodeling.njnu.edu.cn/modelItem/91031f84-7a5c-41e5-a6b8-e3e4ce339b50
    {{htmlJSON.Copy}}

    Contributor(s)
    Initial contribute : 2019-10-14

    {{htmlJSON.CoContributor}}

    Authorship

  • 曹敏
    • :  
    南京师范大学地理科学学院
    :  
    caomin@njnu.edu.cn
    Is authorship not correct? Feed back

    QR Code

    ×
  • {{curRelation.name}}
    {{curRelation.name}}
    {{curRelation.overview}}
    {{curRelation.author.join('; ')}}
    {{curRelation.journal}}





    {{htmlJSON.RelatedItems}}

    {{htmlJSON.LinkResourceFromRepositoryOrCreate}}{{htmlJSON.create}}.

    Drop the file here, orclick to upload.
    Select From My Space
    + add
    {{htmlJSON.Cancel}} {{htmlJSON.OK}}

    {{htmlJSON.authorshipSubmitted}}

    Use My Info Cancel Submit
    Cancel Submit     {{htmlJSON.Cancel}} {{htmlJSON.Submit}}
    {{htmlJSON.Localizations}} + {{htmlJSON.Add}}
    {{ item.label }} {{ item.value }}
    {{htmlJSON.ModelName}}:
    {{htmlJSON.Cancel}} {{htmlJSON.Submit}}     * 名称 别名 {{tag}} +
    系列名 * 版本号 * 目的 * 修改内容 * 创建/修改日期 * 作者
    * 摘要 详细描述
    {{tag}} + 添加关键字
    * 时间参考系
    * 空间参考系类型 * 空间参考系名称

    * 起始日期 终止日期 * 进展 * 开发者
    * 是否开源 * 访问方式 * 使用方式 * 开源协议 * 传输方式 * 获取地址 * 发布日期 * 发布者



    * 编号 * 目的 * 修改内容 * 创建/修改日期 * 作者




    * 时间分辨率 * 时间尺度 * 时间步长 * 时间范围 * 空间维度 * 格网类型 * 空间分辨率 * 空间尺度 * 空间范围
    {{tag}} +     * 类型
    图例

    * 名称 * 描述
    示例描述 * 名称 * 类型 * 值/链接 或 上传


    {{htmlJSON.Cancel}} {{htmlJSON.Submit}}
    Title Author Date Journal Volume(Issue) Pages Links Doi Operation
    {{htmlJSON.Cancel}} {{htmlJSON.Submit}}
    {{htmlJSON.EnterDoiClickSearch}}
    {{htmlJSON.Add}} {{htmlJSON.Cancel}}

    {{articleUploading.title}}

    Authors:  {{articleUploading.authors[0]}}, {{articleUploading.authors[1]}}, {{articleUploading.authors[2]}}, et al.

    Journal:   {{articleUploading.journal}}

    Date:   {{articleUploading.date}}

    Page range:   {{articleUploading.pageRange}}

    Link:   {{articleUploading.link}}

    DOI:   {{articleUploading.doi}}

    Yes, this is it Cancel

    The article {{articleUploading.title}} has been uploaded yet.

    OK     {{htmlJSON.Cancel}} {{htmlJSON.Confirm}}