As a new form of sharing economy, the dockless shared bicycles have rapidly become another new type of public transportation after the bus and subway due to its features such as ride-on-stop, flexible and easy to use, low price, and environmental protection. Nowadays, more and more residents choose to use dockless shared bicycles as a travel tool. However, during the development of dockless shared bicycles, problems such as the imbalance of supply and demand, random parking, and other problems occurred. In order to make better use of the complementary role of shared bicycles in urban transportation, we have constructed a prediction model for rental and return of dockless shared bicycles named QPSO-LSTM, which aims to predict the number of future rental and return of shared bicycles , to effectively understand their possible distribution in the future, and to provide a reference basis for the rebalancing of the distribution of dockless shared bicycles.

The QPSO-LSTM model mainly includes two core algorithms, namely QPSO(quantum particle swarm optimization)(Sun et al. 2004) and LSTM(Long Short-Term Memory)(S. Hochreiter et al. 1997).

(1) QPSO is an improvement on traditional particle swarm optimization (PSO). It is inspired by the theory of quantum physics, that is, all particles have quantum behavior. Based on PSO, this algorithm eliminates the attribute of particle movement direction, that is, the update of particle position is independent of the previous particle position. It is more likely to obtain the global optimal solution or approximate optimal solution and determine the global optimal position(gbest) and part optimal position(pbest) of the particle by increasing the randomness of the particle's position. QPSO has been widely used in many fields such as function optimization. QPSO-LSTM model has some hyperparameters to be optimized, such as time step, number of hidden layer nodes, batch size, etc., as shown in Figure 1.

Fig.1 Parameters to be optimized in QPSO-LSTM

QPSO can be used to quickly determine the hyperparameter combination suitable for the time prediction model, so as to effectively improve the accuracy of the prediction model. The flowchart of the optimization of the LSTM model with the QPSO optimization algorithm is shown in Figure 2: 

Fig.2 QPSO hyperparameter optimization process

(2)LSTM is designed based on Recurrent Neural Network(RNN) to solve the problem of gradient disappearance in RNN network training, so as to better learn the dependency of long time series data. Compared with RNN, LSTM has not been used to screen the information of previous moments. As a kind of deep learning algorithm for the prediction of serial data, LSTM has a good effect on the prediction of time series data and is widely used in the prediction of stock price, traffic flow and so on. The structure diagram of LSTM is shown in Figure 3.

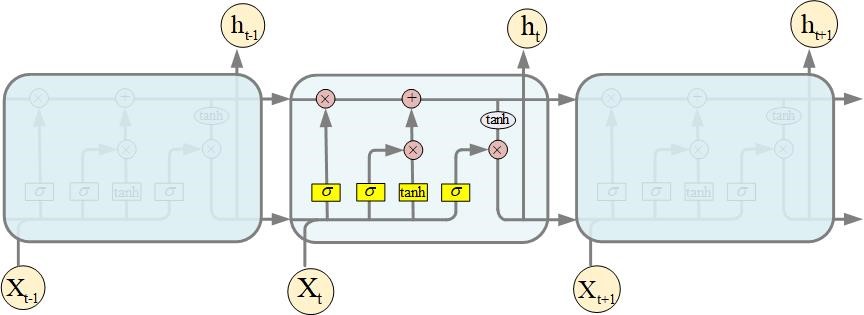
 Fig.3 LSTM structure diagram

In the QPSO-LSTM model, LSTM is used to predict the quantity of dockless shared bicycles rented and returned. The LSTM construction flow chart is shown in Figure 4.

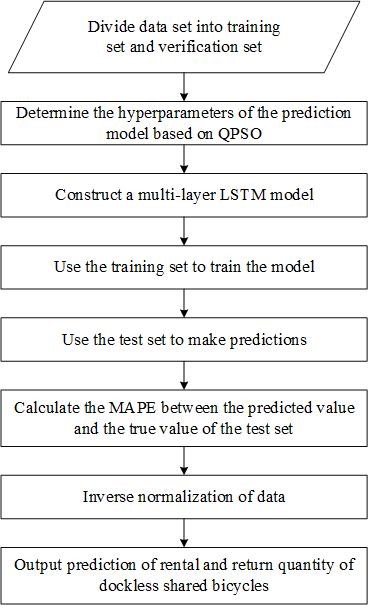
Fig.4 LSTM construction process

[1] Sun Jun, Feng Bin, Xun Wenbo. (2004). Particle swarm optimization with particles having quanturn behavior[J]. Proceedings of Congress on Evolutionary Computation, 325-331

[2] S. Hochreiter, J. Schmidhuber. (1997). Long Short-Term Memory[J]. Neural Computation, 9(8):1735-1780.