(a) The fault structure (line segments) of the Vogtland/northwest Bohemia earthquake swarm region and earthquake epicentres (circles). The main swarm area is marked by the ellipse enclosing the year 2000 swarm activity. (b) The local earthquake magnitudes of this swarm are shown as a function of time elapsed since 2000 August 28.

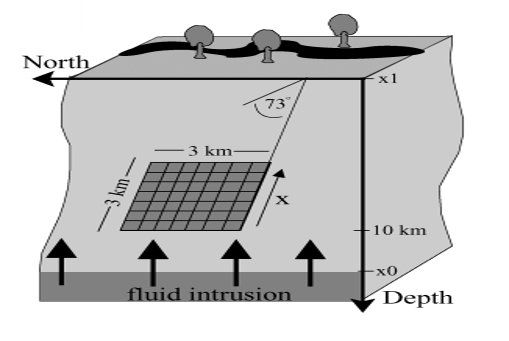
The fault plane of the Vogtland earthquake swarm is modelled with a 3 km × 3 km rectangular patch dipping 73°. The lower edge of the brittle segment is set to a depth of 10 km (see Fig. 2a). The fault is discretized into 50 × 50 cells of dimension 60 m × 60 m each. Earthquake slip occurs when the Coulomb failure stress (CFS) becomes positive at one cell, i.e. the Coulomb failure criterion is fulfilled (Harris 1998):

(1)

Here τ defines the shear and σ the normal stress (positive for compression), P is the pore pressure and μ is the coefficient of friction. Earthquake slip on the fault affects neither the normal stress nor the mean stress on the fault plane. Thus, slip has no effect on the pore pressure if material properties (e.g. permeability) are constant. In contrast, fluid flow generally influences not only the pore pressure but also the stress field. However, because of the numerical costs that would be involved in modelling the full coupling, it is assumed here that the stress field is, to a first order, not influenced by fluid flow (pore pressure changes).

The characteristics of co‐seismic slip are governed by a static/kinetic friction law (Ben‐Zion & Rice 1993). If sliding is initiated, the coefficient of friction μ, i.e. the frictional resistance, drops from its static value μ0 to its lower dynamic value μd and remains there until the earthquake is terminated. The dynamic weakening of the fault strength is accompanied by a drop in stress. The shear stress τ drops to the arrest stress τa which is smaller than the frictional dynamic stress μd(σ−p ) because of dynamic overshoot.

The stress change on the fault plane due to relative slip of one segment is calculated with the analytical solution given by Okada (1992) for an elastic Poisson solid with a rigidity of 30 GPa. For simplification, we assume the slip to always be in the strike direction, although this is not in perfect agreement with the observed Vogtland swarm where both normal and strike‐slip events occurred (Fischer 2003). However, the main characteristics of the model are expected to be independent of this restriction because the stress pattern on the fault changes only slightly for rotating slip on the same fault plane. In particular, the stress decreases inside the rupture zone in the same way, and increases everywhere else. This increase is only slightly larger in the direction of slip.

The sliding of one cell can lead to an instability in other cells, and so on. An earthquake ends when all cells are stable with regard to the Coulomb failure criterion (eq. 1). The duration of earthquakes is much shorter than the typical time separating subsequent earthquakes. Thus we assume instantaneous co‐seismic slip, or, in other words, that the whole earthquake occurs at the same time.

--According to "Seismicity patterns of earthquake swarms due to fluid intrusion and stress triggering"