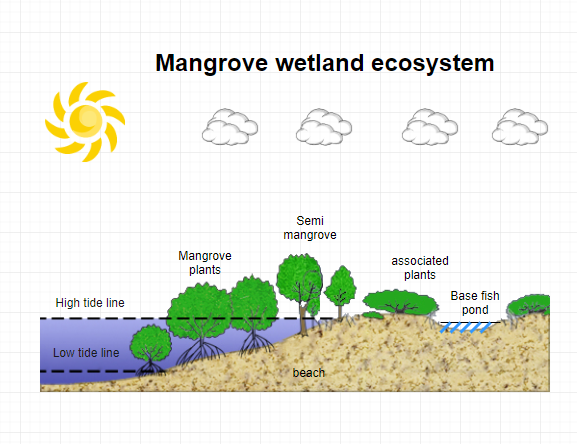
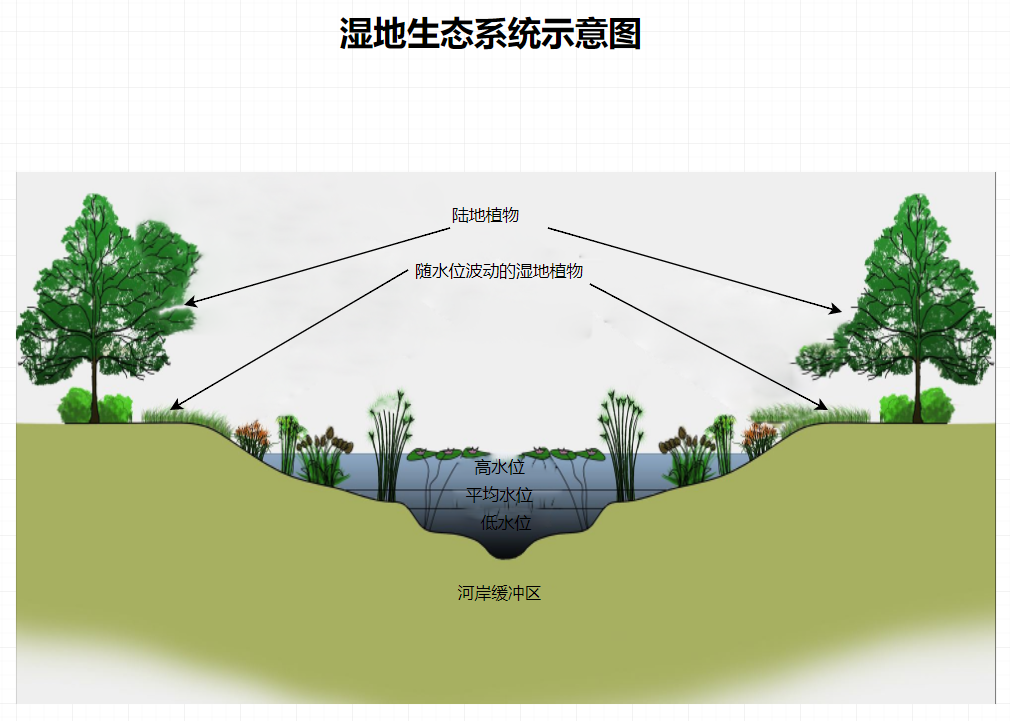
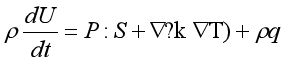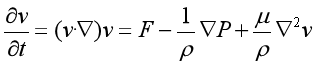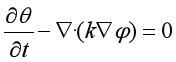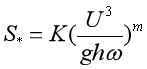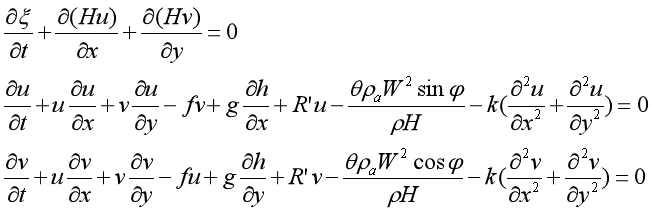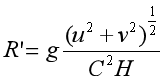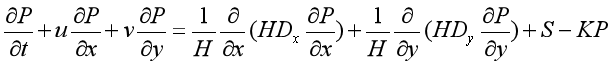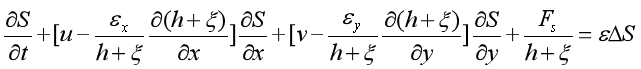湿地水文模型

（1）水文水动力学模型：

连续性方程：

动量方程：

能量方程：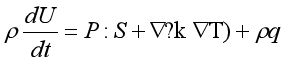

式中，V为流体流速场矢量；ρ为流体的密度；P为流体的应力张量，它是一个有9个分量的物理量，用它可以完全描述场内任一点的应力状况；S为流体的变形速度张量；P:S为流体变形消耗的能量；F为单位流体质点所受到的质量力；U为单位质量流体的内能，是温度的函数；T为流体的温度分布场；k为各方向上的导热率；q为辐射传热率。

地球环境水体运动的描述在许多情况下是通过求解Navier-stocks（简记为N-S）方程来实现。对地面流动的精确描述方法的方程可表示为：

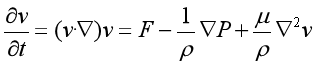
式中，v为空间速度矢量；μ为流体动力黏滞系数，其他变量定义同前。

对地下水流动的描述，采用多孔介质水流运动的达西公式：

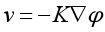
式中，φ为水头的势函数，K为达西函数，v为渗透速度。

如果介质是吸水性的物质，则介质的含水量和渗透速度有关，相应方程为：

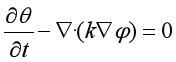
式中，θ为渗透水量。

（2）泥沙冲淤模型：

对于河流以悬移为主的输运过程，泥沙运动及其床面冲淤变化的基本方程为：

泥沙连续方程：

水流挟沙力方程：

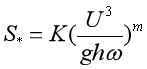
河床变形方程：

对于浅水平面流中的泥沙运动可以采取下列方程描述：

以上各式中，S为含沙量；S_水为泥沙冲淤平衡是对应的含沙量；ω为泥沙沉降速度；h和H分别为河流和浅水流动水深；z₀为河床高程；D_x和D_y为沿纵向（x向）和横向（y向）的扩散系数。

（3）潮流湿地水动力学模型：

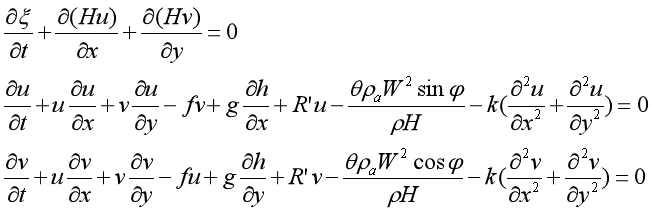
式中，ξ为潮位，h为水底距离坐标平面的距离，即平均水深；H（=h+ξ），为实际水深；u和v分别为沿x和y方向上深度平均流速，其定义可表达为；f为科氏力系数，f=2ΦRcosΦsinΦ/86400，Φ为所在点的纬度；R为地球的半径；g为重力加速度；R’为底面切应力系数；W为风速；θ为风应力系数；φ为风速方向和y轴正方向的夹角；ρ为水的密度；ρ_a为空气密度；k为垂向的紊动交换系数。

由于切应力梯度造成的作用力包括底摩擦应力、自由表面应力和紊动应力，底摩擦应力（R’_u和R’_v）可通过底摩擦应力系数R’来确定，如常用的底摩擦二次方率公式：

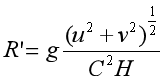
式中，C为谢才系数。

（4）潮流湿地水质模型：

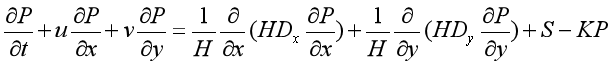
式中，P为污染物沿垂向平均浓度；u，v分别为水体垂向平均后沿x，y方向的流速；H为水深；D_x和D_y分别为x和y方向的分散系数；K为污染物的降解率；S为污染强度。

一般的，计算的初始条件可以根据现状监测资料给出：

闭边界条件为：

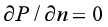
式中，n为闭边界外法线方向。

在开边界处，第一边值的实测资料很难获得。因此，可以认为在海湾涨潮入流阶段，流入的是纯净海水（或污染浓度不变的海水）；落潮出流阶段，假定只有平流运输，边界无污染源，即开边界条件为：

分散系数D_x和D_y通常可以采用经验公式确定（如Elder公式等）。

（5）潮流湿地的泥沙模型：

对于不考虑异重流的简单情形，在波浪和潮流共同作用下的泥沙冲淤基本方程包括：

泥沙连续方程：

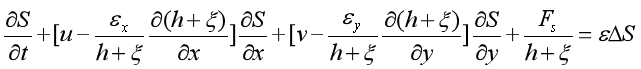
海底变形方程：

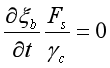
式中，F_s为海底泥沙冲淤函数，其可表达式为F_s=ω_s-ε_z（δS/δ_z）；ε为悬沙在水流中的扩散系数；ω_s为泥沙的沉降速度；ε_x,ε_y和ε_z分别为泥沙在x,y和z方向上的紊动扩散系数：ΔS为泥沙的源汇项；ξ_b为海底床面坐标；γ_c为泥沙干容量。

结合水动力学方程，给定适当的边界条件，即可求解未知量ξ_b，F_s和S。

殷康前，倪晋仁：湿地综合分类研究：Ⅱ.模型，自然资源学报，1998，13（4）