Quoted from: http://image.diku.dk/imagecanon/material/cortes_vapnik95.pdf

Overview

Problems in machine learning often suffer from the curse of dimensionality — each sample may consist of a huge number of potential features (for instance, there can be 162,336 Haar features, as used by the Viola–Jones object detection framework, in a 24×24 pixel image window), and evaluating every feature can reduce not only the speed of classifier training and execution, but in fact reduce predictive power. Unlike neural networks and SVMs, the AdaBoost training process selects only those features known to improve the predictive power of the model, reducing dimensionality and potentially improving execution time as irrelevant features don't need to be computed.

Training

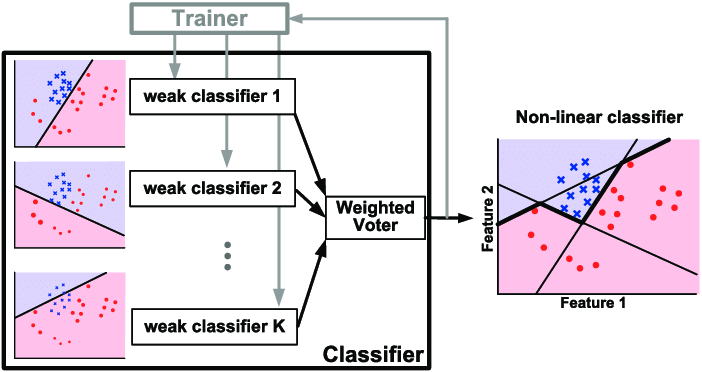
AdaBoost refers to a particular method of training a boosted classifier. A boost classifier is a classifier in the form

{\displaystyle F_{T}(x)=\sum _{t=1}^{T}f_{t}(x)\,\!}

where each {\displaystyle f_{t}} is a weak learner that takes an object {\displaystyle x} as input and returns a value indicating the class of the object. For example, in the two-class problem, the sign of the weak learner output identifies the predicted object class and the absolute value gives the confidence in that classification. Similarly, the {\displaystyle T}th classifier is positive if the sample is in a positive class and negative otherwise.

Each weak learner produces an output hypothesis, {\displaystyle h(x_{i})}, for each sample in the training set. At each iteration {\displaystyle t}, a weak learner is selected and assigned a coefficient {\displaystyle \alpha _{t}} such that the sum training error {\displaystyle E_{t}} of the resulting {\displaystyle t}-stage boost classifier is minimized.

{\displaystyle E_{t}=\sum _{i}E[F_{t-1}(x_{i})+\alpha _{t}h(x_{i})]}

Here {\displaystyle F_{t-1}(x)} is the boosted classifier that has been built up to the previous stage of training, {\displaystyle E(F)} is some error function and {\displaystyle f_{t}(x)=\alpha _{t}h(x)} is the weak learner that is being considered for addition to the final classifier.

Weighting

At each iteration of the training process, a weight {\displaystyle w_{i,t}} is assigned to each sample in the training set equal to the current error {\displaystyle E(F_{t-1}(x_{i}))} on that sample. These weights can be used to inform the training of the weak learner, for instance, decision trees can be grown that favor splitting sets of samples with high weights.

Derivation

This derivation follows Rojas (2009):

Suppose we have a data set {\displaystyle \{(x_{1},y_{1}),\ldots ,(x_{N},y_{N})\}} where each item {\displaystyle x_{i}} has an associated class {\displaystyle y_{i}\in \{-1,1\}}, and a set of weak classifiers {\displaystyle \{k_{1},\ldots ,k_{L}\}} each of which outputs a classification {\displaystyle k_{j}(x_{i})\in \{-1,1\}} for each item. After the {\displaystyle (m-1)}-th iteration our boosted classifier is a linear combination of the weak classifiers of the form:

{\displaystyle C_{(m-1)}(x_{i})=\alpha _{1}k_{1}(x_{i})+\cdots +\alpha _{m-1}k_{m-1}(x_{i})}

Where the class will be the sign of {\displaystyle C_{(m-1)}(x_{i})}. At the {\displaystyle m}-th iteration we want to extend this to a better boosted classifier by adding another weak classifier {\displaystyle k_{m}}, with another weight {\displaystyle \alpha _{m}}:

{\displaystyle C_{m}(x_{i})=C_{(m-1)}(x_{i})+\alpha _{m}k_{m}(x_{i})}

So it remains to determine which weak classifier is the best choice for {\displaystyle k_{m}}, and what its weight {\displaystyle \alpha _{m}} should be. We define the total error {\displaystyle E} of {\displaystyle C_{m}} as the sum of its exponential loss on each data point, given as follows:

{\displaystyle E=\sum _{i=1}^{N}e^{-y_{i}C_{m}(x_{i})}=\sum _{i=1}^{N}e^{-y_{i}C_{(m-1)}(x_{i})}e^{-y_{i}\alpha _{m}k_{m}(x_{i})}}

Letting {\displaystyle w_{i}^{(1)}=1} and {\displaystyle w_{i}^{(m)}=e^{-y_{i}C_{m-1}(x_{i})}} for {\displaystyle m>1}, we have:

{\displaystyle E=\sum _{i=1}^{N}w_{i}^{(m)}e^{-y_{i}\alpha _{m}k_{m}(x_{i})}}

We can split this summation between those data points that are correctly classified by {\displaystyle k_{m}} (so {\displaystyle y_{i}k_{m}(x_{i})=1}) and those that are misclassified (so {\displaystyle y_{i}k_{m}(x_{i})=-1}):

{\displaystyle E=\sum _{y_{i}=k_{m}(x_{i})}w_{i}^{(m)}e^{-\alpha _{m}}+\sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}e^{\alpha _{m}}}

{\displaystyle =\sum _{i=1}^{N}w_{i}^{(m)}e^{-\alpha _{m}}+\sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}(e^{\alpha _{m}}-e^{-\alpha _{m}})}

Since the only part of the right-hand side of this equation that depends on {\displaystyle k_{m}} is {\displaystyle \sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}}, we see that the {\displaystyle k_{m}} that minimizes {\displaystyle E} is the one that minimizes {\displaystyle \sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}} [assuming that {\displaystyle \alpha _{m}>0}], i.e. the weak classifier with the lowest weighted error (with weights {\displaystyle w_{i}^{(m)}=e^{-y_{i}C_{m-1}(x_{i})}}).

To determine the desired weight {\displaystyle \alpha _{m}} that minimizes {\displaystyle E} with the {\displaystyle k_{m}} that we just determined, we differentiate:

{\displaystyle {\frac {dE}{d\alpha _{m}}}={\frac {d(\sum _{y_{i}=k_{m}(x_{i})}w_{i}^{(m)}e^{-\alpha _{m}}+\sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}e^{\alpha _{m}})}{d\alpha _{m}}}}

Setting this to zero and solving for {\displaystyle \alpha _{m}} yields:

{\displaystyle \alpha _{m}={\frac {1}{2}}\ln \left({\frac {\sum _{y_{i}=k_{m}(x_{i})}w_{i}^{(m)}}{\sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}}}\right)}

We calculate the weighted error rate of the weak classifier to be {\displaystyle \epsilon _{m}=\sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}/\sum _{i=1}^{N}w_{i}^{(m)}}, so it follows that:

{\displaystyle \alpha _{m}={\frac {1}{2}}\ln \left({\frac {1-\epsilon _{m}}{\epsilon _{m}}}\right)}

which is the negative logit function multiplied by 0.5.

Thus we have derived the AdaBoost algorithm: At each iteration, choose the classifier {\displaystyle k_{m}}, which minimizes the total weighted error {\displaystyle \sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}}, use this to calculate the error rate {\displaystyle \epsilon _{m}=\sum _{y_{i}\neq k_{m}(x_{i})}w_{i}^{(m)}/\sum _{i=1}^{N}w_{i}^{(m)}}, use this to calculate the weight {\displaystyle \alpha _{m}={\frac {1}{2}}\ln \left({\frac {1-\epsilon _{m}}{\epsilon _{m}}}\right)}, and finally use this to improve the boosted classifier {\displaystyle C_{m-1}} to {\displaystyle C_{m}=C_{(m-1)}+\alpha _{m}k_{m}}.