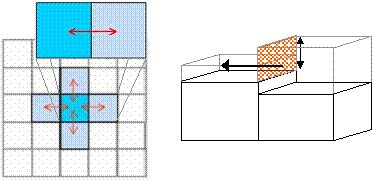
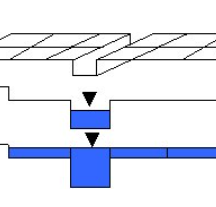
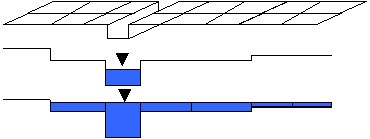
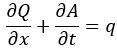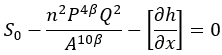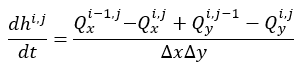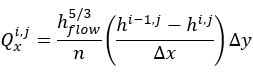LISFLOOD-FP is a coupled 1D/2D hydraulic model based on a raster grid. Effectively, flooding is treated using an intelligent volume-filling process based on hydraulic principles and embodying the key physical notions of mass conservation and hydraulic connectivity.

Channel flow

Channel flow is handled using a one-dimensional approach that is capable of capturing the downstream propagation of a floodwave and the response of flow to free surface slope, which can be described in terms of continuity and momentum equations as:

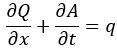
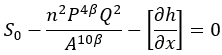
where Q is the volumetric flow rate in the channel, A the cross sectional area of the flow, q the flow into the channel from other sources (i.e. from the floodplain or possibly tributary channels),  the down-slope of the bed, n the Manning’s coefficient of friction, P the wetted perimeter of the flow, and h the flow depth. For problems with no channels present this function can simply be switched off.

The term in brackets in Eq. 2 is the diffusion wave term, which forces the channel flow to respond to both the bed slope and the free surface slope. This can be switched on or off in the model to enable both kinematic and diffusion wave approximations to be tested. Eq's 1 and 2 are discretized using finite differences and a fully implicit scheme for the time dependence.

Channel discretization

Multiple linked tributary channels can be modelled and each is discretized as a single vector along its centreline separate from the overlying floodplain raster grid. These channels may then be linked to simulate whole drainage networks. At each point along each channel vector the required parameters are the width, Manning’s n value and bed elevation. The latter gives the bed slope and also the bankfull depth when the channel vector is combined with the floodplain Digital Elevation Model (DEM). Each channel parameter can be specified at each point along the vector and the model linearly interpolates between these. This interpolated channel is then used to identify cells in the overlying floodplain grid which have a channel lying beneath them.

Floodplain flow

When bankfull depth is exceeded, water is transferred from the channel to the overlying floodplain grid. Floodplain flows are similarly described in terms of continuity and momentum equations, discretized over a grid of square cells, which allows the model to represent 2-D dynamic flow fields on the floodplain. We assume that the flow between two cells is simply a function of the free surface height difference between those cells:

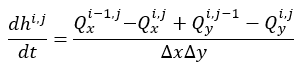
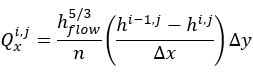
where h i,j is the water free surface height at the node (i,j), Dx and Dy are the cell dimensions, n is the effective grid scale Manning’s friction coefficient for the floodplain, and Qx and Qy describe the volumetric flow rates between floodplain cells. Qy is defined analogously to Qx. The flow depth, h flow, represents the depth through which water can flow between two cells, and is defined as the difference between the highest water free surface in the two cells and the highest bed elevation (this definition has been found to give sensible results for both wetting cells and for flows linking floodplain and channel cells).