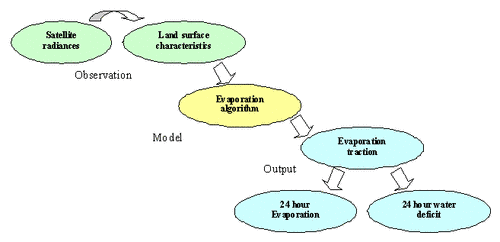
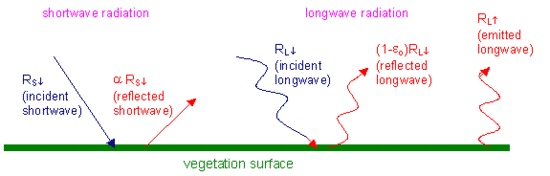
In Eq. (2), the amount of net short-wave radiation (RS↓ - aRS↓) that remains available at the surface, is a function of the surface albedo (a). The broad band surface albedo a is derived from the narrow band spectral reflectances a(λ) measured by each satellite band. The incoming short-wave radiation (RS↓) is computed using the solar constant, the solar incidence angle, a relative earth-sun distance, and a computed broad band atmospheric transmissivity. This latter transmissivity can be estimated from sunshine duration or inferred from pyranometer measurements (if available). The incoming long wave radiation (RL↓) is computed using a modified Stefan-Boltzmann equation with an apparent emissivity that is coupled to the shortwave atmospheric transmissivity and a measured air temperature. Outgoing long wave radiation (RL↑) is computed using the Stefan-Boltzmann equation with a calculated surface emissivity and surface temperature. Surface temperatures are computed from the satellite measurements of thermal radiances.
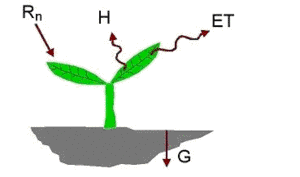
In Eq. (1), the soil heat flux (G) and sensible heat flux (H) are subtracted from the net radiation flux at the surface (Rn) to compute the "residual" energy available for evapotranspiration (λE). Soil heat flux is empirically calculated as a G/Rn fraction using vegetation indices, surface temperature, and surface albedo. Sensible heat flux is computed using wind speed observations, estimated surface roughness, and surface to air temperature differences that are obtained through a sophisticated self-calibration between dry (λE≈0) and wet (H≈0) pixels. SEBAL uses an iterative process to correct for atmospheric instability caused by buoyancy effects of surface heating.
The λE time integration in SEBAL is split into two steps. The first step is to convert the instantaneous latent heat flux (λE) into daily λE24 values by holding the evaporative fraction constant. The evaporative fraction EF is:
EF = λE/ (Rn - G) (-) (3)
Field measurements under various environmental circumstances have indicated that EF behaves temporally stable during the diurnal cycle. Since EF ~ EF24, i.e. the 24 hour latent heat flux can be determined as:
λE24 = EF Rn24 (W/m2) (4)
For simplicity, the 24 hour value of G is ignored in Eq. (4). The second step is the conversion from a daily latent heat flux into monthly values, which has been achieved by application of the Penman-Monteith equation:
λEPM = (sa Rn24 + ρacp Δe/ra) / (sa + γ (1 + rs/ra)) (W/m2) (5)
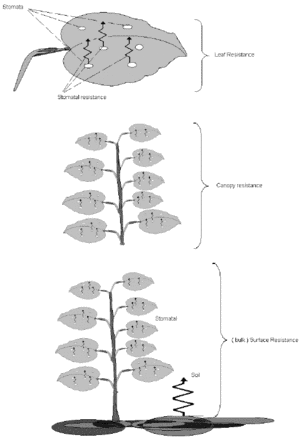
where sa (mbar/K) is the slope of the saturated vapor pressure curve, ρacp (J/m3 K) is the air heat capacity, Δe (mbar) is the vapor pressure deficit, γ (mbar/K) is the psychrometric constant and ra (s/m) is the aerodynamic resistance. The parameters sa, Δe and ra are controlled by meteorological conditions, and Rn and rs by the hydrological conditions.
The SEBAL computations can only be executed for cloudless days. The result of λE24 from Eq. (4) has been explored to convert the Penman-Monteith equation (5) and to quantity rs inversely using λE24= λEPM. The spatial distribution of rs so achieved, will consequently be used to compute λE24 by means of Eq. (5) for all days without satellite image available (Bastiaanssen and Bandara, 2001). The total ETact for a given period can be derived from the longer term average λE flux by correcting for the latent heat of vaporization and the density of water.
SEBAL Biomass growth
The biomass production routine in SEBAL is based on solar radiation absorption by chlorophyll and the conversion of this energy into a dry matter production by means of a light use efficiency:
Bio = APAR(t) e(t) dt (kg/ha) (6)
The absorption of solar radiation (APAR) for photosynthesis depends on global radiation and light interception. The second component of Eq. (6) describes the light use efficiency e(t) that converts energy into dry matters.
Photosynthetic Active Radiation (PAR) (0.4 to 0.7 µm) is part of the short wave solar radiation (0.3 to 3.0 µm) that is absorbed by chlorophyll for photosynthesis in the plants. PAR is thus a fraction of the incoming solar radiation, Rs↓. The PAR value describes the total amount of radiation available for photosynthesis if leaves intercept all radiation. This is a rather theoretical value, because leaves transmit and reflect solar radiation. Only a fraction of PAR will be absorbed by the canopy (APAR) and used for carbon assimilation. APAR can be approximated as a fraction of the PAR using the Normalized Difference Vegetation Index (NDVI):
APAR = (-0.161 + 1.275 NDVI) * PAR (W/m2) (7)