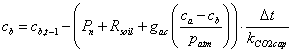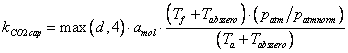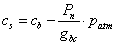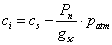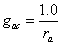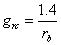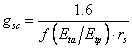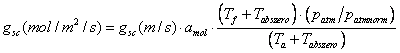The Farquhar biochemical growth model (Farquhar et al., 1980) calculates photosynthesis as a function of demand and supply of CO2. The advantage with this model is that photosynthesis is regulated not only by radiation and transpiration, but also by air humidity, leaf temperature, CO2 availability and leaf nitrogen content, and the plant also experience radiation saturation at high levels of radiation. To function properly, driving variables need to be given as input to the simulation at least once an hour. In this module photosynthesis, P, is calculated as mole carbon per leaf area per second. Thus, P has to be converted to g carbon per unit soil area per day, CAtm→a, at the end of the module:
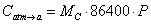 (5.14)
(5.14)
where MC is the molar mass of carbon.
Parameters and variables used in the photosynthesis model are converted in a similar manner.
There are several viewing functions that illustrate the Farquhar photosynthesis model, e.g. Farquhar model – Carbon dioxide pressure as a function of time, Farquhar model – Photosynthesis as a function of carbon dioxide pressure in the sub-stomatal cavity, Farquhar model – Photosynthesis as a function of LAIand Farquhar model – Photosynthesis as a function of radiation.
Three types of photosynthesis are calculated: Rubisco limited photosynthesis, PV, and RuBP limited photosynthesis, PJ and TPU limited photosynthesis, PS. Gross photosynthesis, P, (including photorespiration) will be determined by the most limiting photosynthesis process.
PV, is the Rubisco (leaf enzyme) or carboxylation limited rate of assimilation, which is a function of light, leaf nitrogen, leaf temperature and soil moisture. Photosynthesis as a function of internal CO2 concentration is calculated according to:
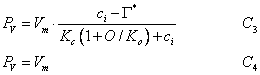 (5.15)
(5.15)
where Vm is a function of the maximum activity of Rubisco, ci is the sub-stomatal cavity concentration of carbon dioxide, Γ* is the CO2 compensation point in the light in the absence of mitochondrial respiration, Kc is the Michaelis-Menten constant of Rubisco for CO2, O is the oxygen concentration (partial pressure) in the atmosphere and Ko is the Michaelis-Menten constant of Rubisco for O2. The reason for the difference between C3 and C4 plants, is that photorespiration occurs in C3 plants at low levels of CO2.
The CO2 compensation point in the absence of mitochondrial respiration, Γ*, is calculated as:
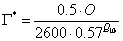 (5.16)
(5.16)
where the Q10 value is calculated from the leaf temperature, Tl:
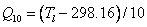 (5.17)
(5.17)
The Michaelis-Menten constant of Rubisco for CO2, Kc, is calculated as:
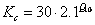 (5.18)
(5.18)
and the Michaelis-Menten constant of Rubisco for O2, Ko, is calculated as:
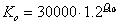 (5.19)
(5.19)
Vm, is a function of the potential maximum capacity of Rubisco, Vmax and the response functions for leaf temperature, f(Tl), leaf carbon nitrogen ratio, f(CNl) and soil moisture, f(Eta/Etp) described above (Eqs. (5.11) -(5.12)):
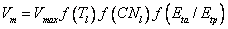 (5.20)
(5.20)
PJ is the RuBP regeneration limited (i.e. light-limited) rate of photosynthesis calculated as:
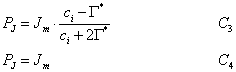 (5.21)
(5.21)
where Jm is calculated as:
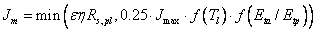 (5.22)
(5.22)
where ε is the quantum efficiency, η is the conversion factor for biomass to carbon, Rs,pl is the absorbed short-wave radiation by the plant and Jmax is the maximum electron transport rate.
Finally, the metabolism of end product limited (TPU limited) rate of photosynthesis, PS, is calculated as:
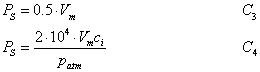 (5.23)
(5.23)
where patm is the atmospheric pressure at the surface.
The maximum Rubisco capacity for the bulk canopy per leaf area, Vmax, can be calculated using equations similar to Beer’s law:
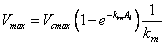 (5.24)
(5.24)
where Vcmax is the maximum Rubisco capacity per leaf area at the top the canopy respectively, krn is the extinction coefficient for net radiation and Al is the leaf area index. The relationship between Vcmax and the maximum electron transportation rate a the top of the canopy, Jcmax, has been investigated by Wohlfahrt et al. (1999). They found that a the ratio between the two was relatively constant (Jcmax / Vcmax = 2.1) for a number of leaves. This relationship is used in the CoupModel to determine the maximum electron transportation rate for the bulk canopy per leaf area, Jmax.
To avoid abrupt transition from one limiting rate to another, we apply two quadratic equations on the assimilation rates that are solved for their smaller roots (Collatz et al., 1991):
 (5.25)
(5.25)
where βvj and βps are empirical constants and PS is an intermediate variable equal to the minimum of PV and PJ.
Analogously to Fick’s law of gas diffusion, the supply of CO2 for photosynthesis can be calculated as:
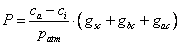 (5.26)
(5.26)
where ca is the external carbon dioxide concentration, patm is the atmospheric pressure at the surface, and gsc is the stomatal , gbc is the boundary layer and gac is the aerodynamic conductances to CO2, respectively. The gas diffusion from the atmosphere to the leaf is calculated step-wise, from the atmosphere, ca, via the canopy air space, cb, to the surface of the leaf, cs, and finally into the sub-stomatal cavity, ci in the following manner:
1) Carbon concentration in the atmosphere, ca: model input.
2) Carbon concentration in the canopy air space, cb:
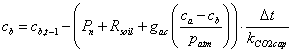 (5.27)
(5.27)
where cb,t-1 is the carbon concentration in the canopy air space from the previous time step, Pn is the net photosynthesis and Rsoil is the sum of all respiration fluxes from the soil surface. kCO2cap is the carbon capacity of air (mol air / m2), which is basically the mass of air under the top of the canopy, or, to be exact, from ground to displacement height. This factor, together with time, t, converts the flows (mol CO2 / m2 / s) into concentrations (mol CO2 / mol air). The carbon capacity is calculated as:
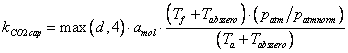 (5.28)
(5.28)
where d is the displacement height, amol is the amount of gas in one cubic meter of air, Tf is the freezing point, Tabszero is the absolute zero temperature, patm is the atmospheric pressure at the soil surface given as a parameter and patmnorm is the normal pressure at the soil surface.
3) Carbon concentration in at the leaf surface, cs:
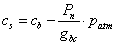 (5.29)
(5.29)
4) Carbon concentration in the sub-stomatal cavity, ci:
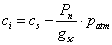 (5.30)
(5.30)
The functions to derive the equilibrium concentration of carbon dioxide in the sub-stomatal cavity, ci, from the demand and the supply functions, follows the iterative procedure in the SiB2 model (Sellers et al., 1996).
The conductance from the canopy air space to the free flowing air for carbon dioxide, gac, is calculated from the aerodynamic resistance to water flow, ra:
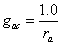 (5.31)
(5.31)
The boundary layer conductance for carbon dioxide, grc, is calculated from the boundary layer resistance for water flow, rb, as:
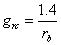 (5.32)
(5.32)
where the boundary layer resistance, rb, is given as an input to model simulations. 1.4 is the ratio of the diffusivities of CO2 and H2O in the leaf boundary layer.
The stomatal conductance for carbon dioxide, gsc, is calculated from the resistance to water flow through stomata, rs, as:
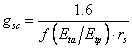 (5.33)
(5.33)
where the response function for soil water stress f(Eta/Etp) is multiplied with the stomatal resistance to account for stomatal closure due to plant water stress. 1.6 is the ratio of the diffusivities of CO2 and H2O in the stomatal pores.
The resistances to water flow are measured in s m-1, and thus corresponding conductance is in m s-1. To convert the conductance from m s-1 to moles m-2 s-1, which is the unit used in the photosynthesis equations, the following conversion is performed:
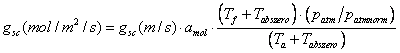 (5.34)
(5.34)
Reduction of photosynthesis due to grain development is simulated in the same way as in the light use efficiency approach, by replacing εL with ε in Eq.(5.13).



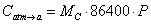 (5.14)
(5.14)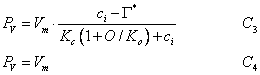
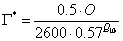
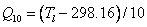
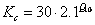
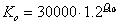
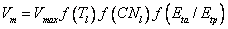
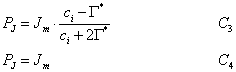
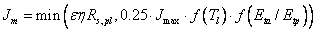
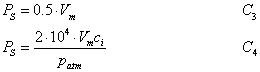 (5.23)
(5.23)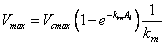

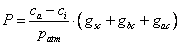 (5.26)
(5.26)