Quoted from:https://scikit-learn.org/stable/modules/biclustering.html#spectral-coclustering

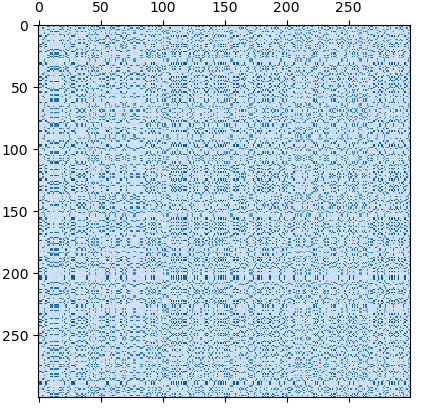
The SpectralCoclustering algorithm finds biclusters with values higher than those in the corresponding other rows and columns. Each row and each column belongs to exactly one bicluster, so rearranging the rows and columns to make partitions contiguous reveals these high values along the diagonal:

Note

The algorithm treats the input data matrix as a bipartite graph: the rows and columns of the matrix correspond to the two sets of vertices, and each entry corresponds to an edge between a row and a column. The algorithm approximates the normalized cut of this graph to find heavy subgraphs.

 

 

Mathematical formulation

An approximate solution to the optimal normalized cut may be found via the generalized eigenvalue decomposition of the Laplacian of the graph. Usually this would mean working directly with the Laplacian matrix. If the original data matrix A has shape m×n, the Laplacian matrix for the corresponding bipartite graph has shape(m+n)×(m+n). However, in this case it is possible to work directly with A, which is smaller and more efficient.

The input matrix A is preprocessed as follows:

Where R is the diagonal matrix with entry i equal to ∑jAij and C is the diagonal matrix with entry j equal to ∑iAij.

The singular value decomposition An=UΣV⊤, provides the partitions of the rows and columns of A. A subset of the left singular vectors gives the row partitions, and a subset of the right singular vectors gives the column partitions.

The ℓ=⌈log2⁡k⌉ singular vectors, starting from the second, provide the desired partitioning information. They are used to form the matrix Z:

where the columns of U are u2,…,uℓ+1, and similarly for V.

Then the rows of Z are clustered using k-means. The first n_rows labels provide the row partitioning, and the remaining n_columns labels provide the column partitioning.

Examples:

1. A demo of the Spectral Co-Clustering algorithm: A simple example showing how to generate a data matrix with biclusters and apply this method to it.

2. Biclustering documents with the Spectral Co-clustering algorithm: An example of finding biclusters in the twenty newsgroup dataset.

References:

• Dhillon, Inderjit S, 2001. Co-clustering documents and words using bipartite spectral graph partitioning.