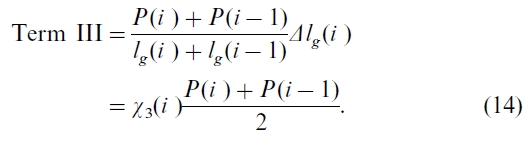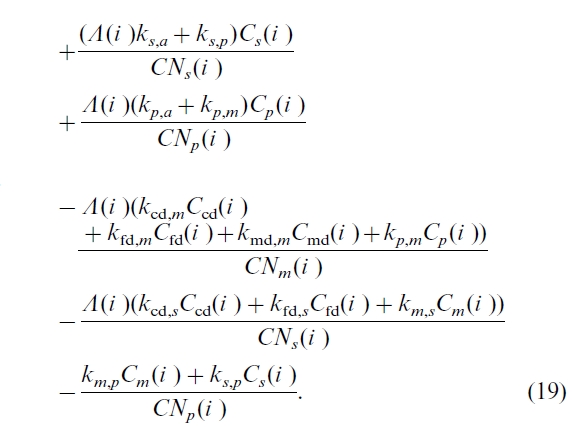1 The response function of NPP to disturbances 
The stand age distribution A(y, i ) can be determined using a Weibull distribution:

where q is the total fire and insect occurrence frequency,  is the gamma function, and s is the shape parameter (Kasischke et al., 1995). We further assume that only mature forests are harvested. At y=0 (i.e. for areas disturbed and yet to regenerate), A(0, i ) was the difference between the disturbed and planted areas in previous n years, where n is the average age that a forest may need to start to regenerate. For example, n=5 for Canada’s forests, with a range of 1–10 years (Bunce, 1989). For each subsequent year, A(y, i ) is calculated by increasing the age by one year for not disturbed forest areas, returning the age to zero for newly disturbed forest areas, and entering age one for previously disturbed forest areas which at that time begin to regenerate. In this study, all areas are treated equally, and no spatial detail is involved. With the calculated A(y, i ) and FNPP(y), the overall effect of disturbances on NPP is then given by
is the gamma function, and s is the shape parameter (Kasischke et al., 1995). We further assume that only mature forests are harvested. At y=0 (i.e. for areas disturbed and yet to regenerate), A(0, i ) was the difference between the disturbed and planted areas in previous n years, where n is the average age that a forest may need to start to regenerate. For example, n=5 for Canada’s forests, with a range of 1–10 years (Bunce, 1989). For each subsequent year, A(y, i ) is calculated by increasing the age by one year for not disturbed forest areas, returning the age to zero for newly disturbed forest areas, and entering age one for previously disturbed forest areas which at that time begin to regenerate. In this study, all areas are treated equally, and no spatial detail is involved. With the calculated A(y, i ) and FNPP(y), the overall effect of disturbances on NPP is then given by
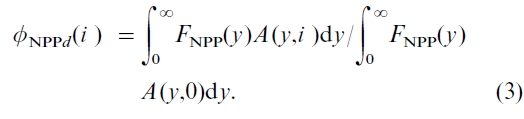

2 The response function of NPP to non-disturbances 
For C3 plants, which include all Canada’s forests species, the instantaneous photosynthesis rate of a single leaf p is limited by the minimum of the two values (Farquhar et al., 1980; Bonan,1995; Luo et al., 1996):

where p1 and p2 are leaf gross photosynthesis limited by electron transport and rubisco activity, respectively. The values of J, Vm, ci, 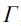 , and kco in Eq. (4) are given by (Sellers et al., 1992; Bonan,1995):
, and kco in Eq. (4) are given by (Sellers et al., 1992; Bonan,1995):
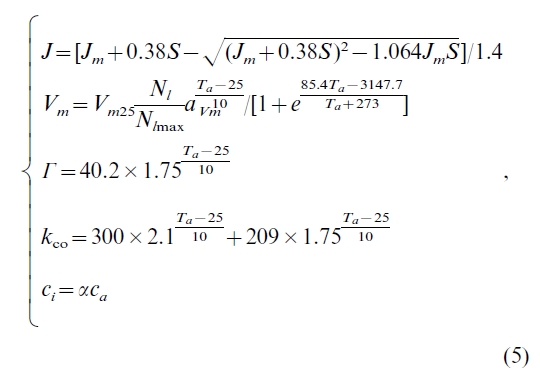
Jm=[Jm25(Nl/Nlmax)ajm(Ta-25)/10]/[1+exp((85.4Ta-3147.7)/(Ta+273))].The meanings of
other terms are listed in Notation. Eq. (5) shows that p is affected by climatic variables (i.e. Ta, S, and hr) and atmospheric variables (i.e. ca and N deposition). The effect of N deposition on p is incorporated through Nl/Nlmax (see details in Section 3).
The area-averaged annual gross photosynthesis rate of a forest region in year i, P(i ), is then given by integrating p for all leaves (x) over the whole forest region (y) and time periods during the year (t)
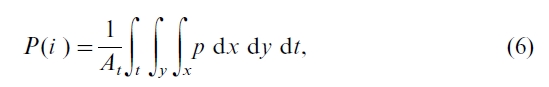 There are many ways to carry out this integration for all leaves in a stand (Norman, 1993). One way, simple yet effective, is to stratify a canopy into sunlit and shaded leaves (Norman, 1993), since Ta, ca, and hr are more or less the same for all leaves in a canopy because canopy air is often well mixed during daytime. This stratification is essential because irradiation changes greatly for different leaves depending on their positions relative to the sun, resulting in different J values for different leaves in the canopy. With this stratification and canopy radiation models (Black et al., 1991; Chen et al., 1999a), we calculate the instantaneous canopy photosynthesis rate, pcan, by the minimum of
There are many ways to carry out this integration for all leaves in a stand (Norman, 1993). One way, simple yet effective, is to stratify a canopy into sunlit and shaded leaves (Norman, 1993), since Ta, ca, and hr are more or less the same for all leaves in a canopy because canopy air is often well mixed during daytime. This stratification is essential because irradiation changes greatly for different leaves depending on their positions relative to the sun, resulting in different J values for different leaves in the canopy. With this stratification and canopy radiation models (Black et al., 1991; Chen et al., 1999a), we calculate the instantaneous canopy photosynthesis rate, pcan, by the minimum of

where Lsun is the sunlit leaf area index, given by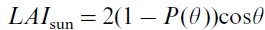 , where
, where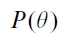 is the gap fraction at the view zenith angle
is the gap fraction at the view zenith angle 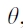 , calculated as
, calculated as 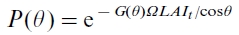 (Nilson, 1971; Chen et al.,1997). The shaded leaf area index, Lshad, thus equals the difference of total leaf area index Lt and Lsun. Assuming no significant changes in morphology of leaves occurred since the industrialization, we can calculate the change in area-averaged Lt in year i by
(Nilson, 1971; Chen et al.,1997). The shaded leaf area index, Lshad, thus equals the difference of total leaf area index Lt and Lsun. Assuming no significant changes in morphology of leaves occurred since the industrialization, we can calculate the change in area-averaged Lt in year i by

The values of J for sunlit leaves and shaded leaves, Jsun and Jshad, are calculated by replacing S in Eq. (5) with Ssun and Sshad respectively, where Ssun and Sshad are calculated following Black et al. (1991) and Chen et al. (1999a).
Assuming fp is the fraction of canopy photosynthesis limited by Pcan1, we calculate the canopy photosynthesis rate over the time period by
 With pcan, we reduce Eq. (6) to
With pcan, we reduce Eq. (6) to
 While it is theoretically possible to calculate P(i) for each year since the industrialization, such an operation is practically limited by data availability. An alternative is to calculate P(i) only for a recent year for which quality data are available, and to determine P(i) in other years using a relationship between the interannual relative change in P(i),(dP(i)/[P(i)di]), and the external forcing factors. Differentiating Eq. (10) gives
While it is theoretically possible to calculate P(i) for each year since the industrialization, such an operation is practically limited by data availability. An alternative is to calculate P(i) only for a recent year for which quality data are available, and to determine P(i) in other years using a relationship between the interannual relative change in P(i),(dP(i)/[P(i)di]), and the external forcing factors. Differentiating Eq. (10) gives
 where term I represents the effect on dP(i)/di caused by changes in pcan(y, t), while term II and III represent, respectively, the effects caused by changes in forest cover area and growing season length (lg). The value of dpcan(y, t) is given by differentiating Eq. (9):
where term I represents the effect on dP(i)/di caused by changes in pcan(y, t), while term II and III represent, respectively, the effects caused by changes in forest cover area and growing season length (lg). The value of dpcan(y, t) is given by differentiating Eq. (9):
 where L1, L2, LT1,1, LT1,2, LT1,3, LN1, LL1,1, LL1,2,LT2,1, LT2,2, LT2,3, LT2,4, LN2, and LL2 are coefficients for the effects of CO2 fertilization, climate variability, N availability, and leaf area changes (see Appendix A). Due to the lack of historical data about changes in hr, Ssun, and Sshad since industrialization, we omit their impacts in this study. All these L terms (shortened as Lx) and pcan vary diurnally and seasonally as well as between locations. Due to the covariance between Lx and pcan, Lx cannot be factored out of the two-dimension integration in Eq. (11). To carry out this integration, detailed data for Lx and pcan are required. In reality, this is not feasible, especially for the long historical periods in this study. To avoid this difficulty, we use a 3-step spatial and temporal scaling algorithm: (1) To replace the integration by a discrete summation; (2) To estimate the discrete summation using the correlation coefficient, r, between the two variables Lx and pcan, namely,
where L1, L2, LT1,1, LT1,2, LT1,3, LN1, LL1,1, LL1,2,LT2,1, LT2,2, LT2,3, LT2,4, LN2, and LL2 are coefficients for the effects of CO2 fertilization, climate variability, N availability, and leaf area changes (see Appendix A). Due to the lack of historical data about changes in hr, Ssun, and Sshad since industrialization, we omit their impacts in this study. All these L terms (shortened as Lx) and pcan vary diurnally and seasonally as well as between locations. Due to the covariance between Lx and pcan, Lx cannot be factored out of the two-dimension integration in Eq. (11). To carry out this integration, detailed data for Lx and pcan are required. In reality, this is not feasible, especially for the long historical periods in this study. To avoid this difficulty, we use a 3-step spatial and temporal scaling algorithm: (1) To replace the integration by a discrete summation; (2) To estimate the discrete summation using the correlation coefficient, r, between the two variables Lx and pcan, namely,

where n is the number of data points in terms of both time periods and spatial locations,  is the spatial and temporal assemble average of Lx in year i, and s is the standard deviation; and (3) To introduce a conversion coefficient,
is the spatial and temporal assemble average of Lx in year i, and s is the standard deviation; and (3) To introduce a conversion coefficient, ,that gives
,that gives
 , where
, where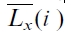 is calculated using annual mean values of climate,
is calculated using annual mean values of climate,
N availability, and CO2 concentration. Using this algorithm, we express term I as follows:

Term II in Eq. (11) is the effect of the change in forest area on the total photosynthesis. Since we consider only the existing forests, and LUC effects are outside the scope of this study. The changes in forest area due to disturbances are considered in Section 1.
Term III in Eq. (11) is the result of growing season length changes, i.e.
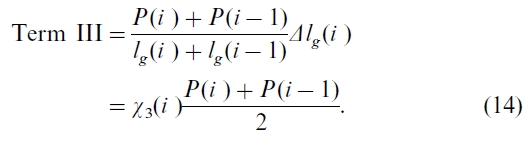
This term can be very important at high latitudes where the growing season is short and air temperature increased at a higher rate than that at low and middle latitudes (Frolking, 1997; Chen et al., 1999b). Inserting Eqs. (13) and (14) into Eq. (11), we calculate the interannual relative change in P(i ) by

So far, we have considered only gross photosynthesis rate P(i ). NPP is only about 25–60% of P(i ), dependent on plant species, because a large part of P(i ) is consumed by autotrophic respiration (Ryan et al., 1997). Yet, the ratio of NPP to P(i ) is conservative with climate change and N status (Ryan et al., 1997), so that

From Eq. (1) and Eqs. (15) and (16), the effects of non-disturbance factors on NPP can then be calculated as
 3 N cycle and leaf N content
3 N cycle and leaf N content
The total available N in the soils in year i, Nav,s(i ), is the sum of atmospheric N deposition
Ndep(i ), biotic N fixation Nfix(i ), and net N mineralization Nmin(i )

We use measured Ndep(i ) values (Ro et al., 1995). The value of Nfix(i ) is calculated based on the studies of Van Cleve and Alexander (1981), Parton et al. (1987), and Chapin and Bledsoe (1992) (see detail in Chen et al., 2000b). Net N mineralization is stochastically related to the C cycle through the C:N ratios and is calculated by:

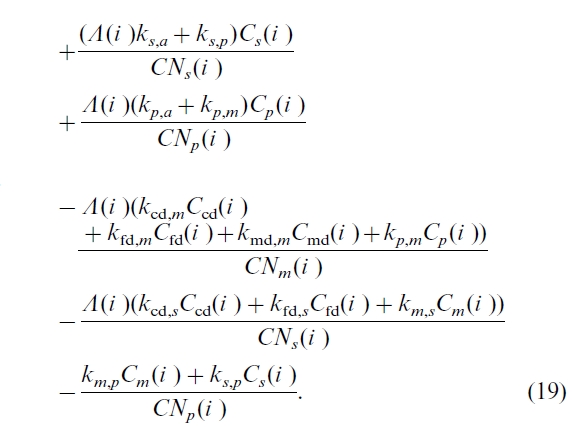
This equation follows the same principle as that of Townsend et al. (1996) and Holland et al. (1997), but differs in two aspects. One is that additional soil C pools are included in this equation. The second aspect is that we allow C/N ratios of biomass and soil C pools to vary, based on recent experimental findings. Many recent studies revealed that when grown in higher CO2, plant issues (including green leaves) had consistently lower N concentration (e.g. Curtis et al., 1995). Yet leaf litter quality is essentially the same under different CO2 levels because N is withdrawn prior to leaf senescence (O’Neill, 1994). In contrast, N in fine roots is not mobilized prior to senescence (Nambiar, 1987), and the C/N ratio was found to be much higher in fine roots grown under higher CO2 environments (Norby, 1994). Experimental evidence also showed that C/N ratios of soil C pools vary from year to year (Schimel et al., 1994), and vary at different N and CO2 levels (Pregitzer et al., 1995). Some recent models (e.g. Schimel et al., 1996; Comins, 1997) have incorporated these experimental findings of varying C/N ratios. In this study, we calculate a C/N ratio for each of the biomass and soil C pools as the ratio of total C content to total N content of the C pool in the year of concern.
Due to N loss as a result of wildfire, harvest, gas emission, and leaching, only a fraction of Nav,s(i ) will be taken up by the plants. The value of Nup(i ) can be determined through solving three related equations: (1) Nav,s(i )=Nup(i )+Nloss(i );(2) a Michaelis–Menten relationship between Nup(i ) and the inorganic N concentration in the soil (Rastetter et al., 1991; Hudson et al., 1994); and (3) a linear relationship between Nloss(i ) and the inorganic N concentration in the soil. The solution for Nup(i ) is given by:

where the maximum uptake capacity Nup,max(i ) is given by b1[Cfr(i )/Cfr(0)] [CNfr(i)/CNfr(0)]-Q10,Nup(Ts (i )-Ts (0))/10, b1 and b2 are constants determined by equaling N input into and export from the forest ecosystems during the pre-industrial periods. In addition to the Nup(i ), the N transferred from senesced leaves in year i-1, Ntr(i ), also contributes to the total available N in plants in year i, Nav,p(i ).
We use the same coefficients partitioning Nav,p to green leaf, fine roots, wood, and coarse roots in year i as in year i-1 because there is no evidence that these coefficients vary in one way or another. Equations for calculating C/N ratio of green leaf, fine roots, wood, coarse roots, fine structure detritus, coarse structure detritus, and slow soil C are given in Appendix A. The C/N ratios of microbe, metabolic detritus, passive soil C, and charcoal are assumed to be constant. With the known values of CNl(i ) and Lt(i ), and Cl(i ), the mean leaf N content per unit leaf area at year i, Nl(i ), can be calculated as follows

where the value of Nl(i ) is constrained to 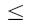 Nlmax(i ). Since the relationship between age and NPP is empirically pre-determined, the interactions between changes in NPP caused by age class shift and N cycle have already been included in the age–NPP relationship. Therefore, the value of Nl(i ) is calculated after considering only the climatic and atmospheric changes.
Nlmax(i ). Since the relationship between age and NPP is empirically pre-determined, the interactions between changes in NPP caused by age class shift and N cycle have already been included in the age–NPP relationship. Therefore, the value of Nl(i ) is calculated after considering only the climatic and atmospheric changes.
4 C cycle
The change in the size of each C pool in InTEC is described by the first-order rate kinetics (Paul and Clark, 1996)
 where Input(i ) is a fraction of NPP transferred to biomass C pools or a fraction of upstream C pools to soil and forest product C pools. It is important to note that if inventory-based Cx(i ) and estimated NPP are used, which can only be measured or estimated with limited accuracy, a large error can be introduced in
where Input(i ) is a fraction of NPP transferred to biomass C pools or a fraction of upstream C pools to soil and forest product C pools. It is important to note that if inventory-based Cx(i ) and estimated NPP are used, which can only be measured or estimated with limited accuracy, a large error can be introduced in  , which is usually much smaller than NPP or kx(i )Cx(i ) in a given year. To avoid this error, we rearrange Eq. (22) by taking Cx(i ) as Cx(i-1)+
, which is usually much smaller than NPP or kx(i )Cx(i ) in a given year. To avoid this error, we rearrange Eq. (22) by taking Cx(i ) as Cx(i-1)+ , so that
, so that
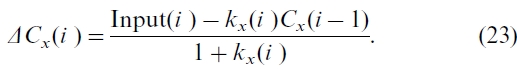
To calculate Cx(i-1), Cx(i-2) and NPP(i-1) are needed. This procedure continues, until the pre-industrial period is reached during which we assume  under the mean disturbance rates and climatic and atmospheric conditions. This procedure shows that
under the mean disturbance rates and climatic and atmospheric conditions. This procedure shows that  depends on historical changes in disturbance rates and climatic conditions over the entire time period since the industrialization. Following this procedure, the changes in biomass, soil, and forest products C pools are calculated by subtracting C output terms (i.e. transfer to downstream pools, and fire emission, oxidation, and respiration to the atmosphere) from the input terms (i.e. fraction of NPP partitioned to the C pool concerned, and C transfer from upstream pools). Farquhar and Henry (1997) estimated that -10% of remaining wood after burning will become charcoal instead of Ccd, and we adopt this percentage in this study. The value of Fm(i ) affects the partitioning of leave and fine roots litter to detritus C pools, and is given by Fm(i )=0.85-0.018LN(i ) (Schimel et al., 1996).Equations for calculating changes in biomass, soil, and forest products C pools are given in Appendix A. For the five product pools, the changes in the sizes of lumber (
depends on historical changes in disturbance rates and climatic conditions over the entire time period since the industrialization. Following this procedure, the changes in biomass, soil, and forest products C pools are calculated by subtracting C output terms (i.e. transfer to downstream pools, and fire emission, oxidation, and respiration to the atmosphere) from the input terms (i.e. fraction of NPP partitioned to the C pool concerned, and C transfer from upstream pools). Farquhar and Henry (1997) estimated that -10% of remaining wood after burning will become charcoal instead of Ccd, and we adopt this percentage in this study. The value of Fm(i ) affects the partitioning of leave and fine roots litter to detritus C pools, and is given by Fm(i )=0.85-0.018LN(i ) (Schimel et al., 1996).Equations for calculating changes in biomass, soil, and forest products C pools are given in Appendix A. For the five product pools, the changes in the sizes of lumber ( ), pulp-wood (
), pulp-wood ( ),and landfills (
),and landfills ( ) C pools are calculated also using the first-order rate kinetics in the same way as for ecosystem C pools, while the bio-energy and burned-as-waste release C within a year.
) C pools are calculated also using the first-order rate kinetics in the same way as for ecosystem C pools, while the bio-energy and burned-as-waste release C within a year.
Summation of these C pool changes gives the area-averaged annual C balance or NBP in year i. The cumulative change in each of these C pools is obtained by integrating the change since the industrialization.




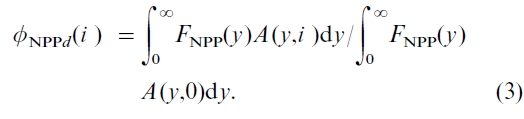


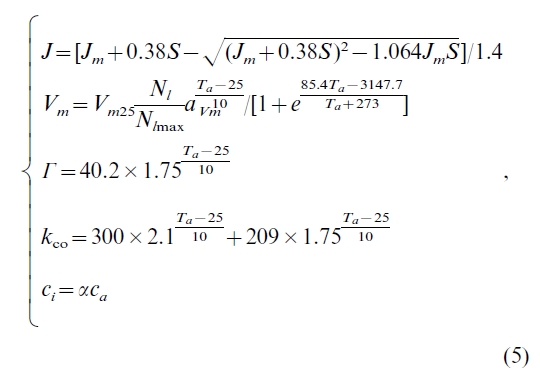
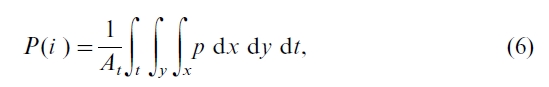 There are many ways to carry out this integration for all leaves in a stand (Norman, 1993). One way, simple yet effective, is to stratify a canopy into sunlit and shaded leaves (Norman, 1993), since Ta, ca, and hr are more or less the same for all leaves in a canopy because canopy air is often well mixed during daytime. This stratification is essential because irradiation changes greatly for different leaves depending on their positions relative to the sun, resulting in different J values for different leaves in the canopy. With this stratification and canopy radiation models (Black et al., 1991; Chen et al., 1999a), we calculate the instantaneous canopy photosynthesis rate, pcan, by the minimum of
There are many ways to carry out this integration for all leaves in a stand (Norman, 1993). One way, simple yet effective, is to stratify a canopy into sunlit and shaded leaves (Norman, 1993), since Ta, ca, and hr are more or less the same for all leaves in a canopy because canopy air is often well mixed during daytime. This stratification is essential because irradiation changes greatly for different leaves depending on their positions relative to the sun, resulting in different J values for different leaves in the canopy. With this stratification and canopy radiation models (Black et al., 1991; Chen et al., 1999a), we calculate the instantaneous canopy photosynthesis rate, pcan, by the minimum of
 While it is theoretically possible to calculate P(i) for each year since the industrialization, such an operation is practically limited by data availability. An alternative is to calculate P(i) only for a recent year for which quality data are available, and to determine P(i) in other years using a relationship between the interannual relative change in P(i),(dP(i)/[P(i)di]), and the external forcing factors. Differentiating Eq. (10) gives
While it is theoretically possible to calculate P(i) for each year since the industrialization, such an operation is practically limited by data availability. An alternative is to calculate P(i) only for a recent year for which quality data are available, and to determine P(i) in other years using a relationship between the interannual relative change in P(i),(dP(i)/[P(i)di]), and the external forcing factors. Differentiating Eq. (10) gives where term I represents the effect on dP(i)/di caused by changes in pcan(y, t), while term II and III represent, respectively, the effects caused by changes in forest cover area and growing season length (lg). The value of dpcan(y, t) is given by differentiating Eq. (9):
where term I represents the effect on dP(i)/di caused by changes in pcan(y, t), while term II and III represent, respectively, the effects caused by changes in forest cover area and growing season length (lg). The value of dpcan(y, t) is given by differentiating Eq. (9): where L1, L2, LT1,1, LT1,2, LT1,3, LN1, LL1,1, LL1,2,LT2,1, LT2,2, LT2,3, LT2,4, LN2, and LL2 are coefficients for the effects of CO2 fertilization, climate variability, N availability, and leaf area changes (see Appendix A). Due to the lack of historical data about changes in hr, Ssun, and Sshad since industrialization, we omit their impacts in this study. All these L terms (shortened as Lx) and pcan vary diurnally and seasonally as well as between locations. Due to the covariance between Lx and pcan, Lx cannot be factored out of the two-dimension integration in Eq. (11). To carry out this integration, detailed data for Lx and pcan are required. In reality, this is not feasible, especially for the long historical periods in this study. To avoid this difficulty, we use a 3-step spatial and temporal scaling algorithm: (1) To replace the integration by a discrete summation; (2) To estimate the discrete summation using the correlation coefficient, r, between the two variables Lx and pcan, namely,
where L1, L2, LT1,1, LT1,2, LT1,3, LN1, LL1,1, LL1,2,LT2,1, LT2,2, LT2,3, LT2,4, LN2, and LL2 are coefficients for the effects of CO2 fertilization, climate variability, N availability, and leaf area changes (see Appendix A). Due to the lack of historical data about changes in hr, Ssun, and Sshad since industrialization, we omit their impacts in this study. All these L terms (shortened as Lx) and pcan vary diurnally and seasonally as well as between locations. Due to the covariance between Lx and pcan, Lx cannot be factored out of the two-dimension integration in Eq. (11). To carry out this integration, detailed data for Lx and pcan are required. In reality, this is not feasible, especially for the long historical periods in this study. To avoid this difficulty, we use a 3-step spatial and temporal scaling algorithm: (1) To replace the integration by a discrete summation; (2) To estimate the discrete summation using the correlation coefficient, r, between the two variables Lx and pcan, namely,