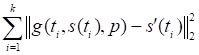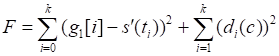Model Classifications 1
Model Classifications 2
| Title | Author | Date | Journal | Volume(Issue) | Pages | Links | Doi | Operation |
|---|